read

Hard things for very deep neural network is training without vanishing or exploding gradient.

One of solution to solve this problem is skip connection.

The idea is feeding an output of activation to the input of deeper layer.

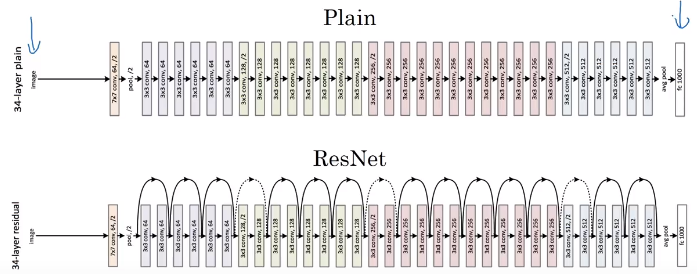
With this idea we can build the trained neural network called ResNet even over 100 layers.

This post is based on the video lecture¹

Residual block

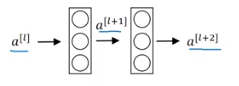
Before explaining the residual block, Let’s see the plain neural network case.

\[a^{[l]} \rightarrow Linear \rightarrow ReLU \xrightarrow{a^{[l+1]}} Linear \rightarrow Relu \rightarrow a^{[l+2]}\]

\[\begin{align} z^{[l+1]}&=W^{[l+1]} \cdot a^{[l]} + b^{[l+1]} \\ a^{[l+1]} &= g(z^{[l+1]}) \\ \\ z^{[l+2]}&=W^{[l+2]} \cdot a^{[l+1]} + b^{[l+2]} \\ a^{[l+2]} &= g(z^{[l+2]}) \end{align}\]

Like the above figure and equation, the output of previous layer is the input of next layer after linear operation and activation.

The idea of residual block is creating shortcut(skip connection) to make shallow layer skip into much deeper network directly.

\[\begin{align} z^{[l+1]}&=W^{[l+1]} \cdot a^{[l]} + b^{[l+1]} \\ a^{[l+1]} &= g(z^{[l+1]}) \\ \\ z^{[l+2]}&=W^{[l+2]} \cdot a^{[l+1]} + b^{[l+2]} \\ a^{[l+2]} &= g(z^{[l+2]} + a^{[l]}) \end{align}\]

Using residual block allows you train much deeper neural network. And It is also helpful for vanishing and exploding gradient problem without appreciable loss performance.

Why ResNets work

Normally, Getting deeper network is getting harder to train neural network.

It will be less true in case of ResNet. But how?

Assuming that, there are two deep neural networks, one with $l​$ layers and other one is $l+2​$ layers.

\[\begin{align} &1. X \rightarrow \fbox{Big NN} \rightarrow a^{[l]} \\ &2. X \rightarrow \fbox{Big NN} \rightarrow a^{[l]} \rightarrow \fbox{layer $l+1$} \rightarrow \fbox{layer $l+2$} \rightarrow a^{[l+2]} \end{align}\]

When we use ReLU as activation function of neural network, $a^{[l]} \ge 0$

\[\require{cancel} \begin{align} a^{[l+2]} &= g(z^{[l+2]} + a^{[l]})\\ &= g(w^{[l+2]}\cdot a^{[l+1]} + b^{[l+1]} + a^{[l]}) \\ \\ &\text{If $w^{[l+2]}=0, b^{[l+1]}=0$ and $g$ is ReLU,} \\ &= g(\cancelto{0}{w^{[l+2]}}\cdot a^{[l+1]} + \cancelto{0}{b^{[l+1]}} + a^{[l]}) \\ &= g(a^{[l]}) \\ & = a^{[l]} \end{align}\]

Like the above equation, even the weight of two added layers is zero, the skip connection from layer $l$ to layer $l+2$ will be trained as an Identity function.

That’s why the added two layers with residual block will not hurt the performance of neural network.

Also, If the extra two layers can be trained well, we will get better performance than learning identity function.

Need to know for implementation

You should know the one more detail of residual network for implementation.

In these equation, $a^{[l+2]}=g(z^{[l+2]} + a^{[l]})$ , $z^{[l+2]}$ and $a^{[l]}$ must be same dimensions.

So you should define the same convolutions for two values to make the dimensions equal.

Because same convolution preserves dimensions and so it make it easier carry out to have shortcut.

In case the two vectors, $z^{[l+2]}$ and $a^{[l]}$, have different dimensions, you have to define the zero padded or trainable matrix $w_s$ to make $a^{[l]}$ have same dimension like $z^{[l+2]}$ by vector product, $w_s \cdot a^{[l]}$.

\[a^{[l+2]}=g(z^{[l+2]} + w_s \cdot a^{[l]})\]

In the above figure, the same dimension can be added in residual block. However, the shortcut from a layer before the pooling to a layer after pooling can be added after vector product with $w_s$ which adjust the dimension of layers same.

1. https://www.coursera.org/learn/neural-networks-deep-learning?specialization=deep-learning ↩