read

Assuming that we need to make a model considering sequential input like previous input can have an effect on next input. Then, Depending on the time and partial input, the output can be affected.

In this post i will introduce RNN that is powerful neural network to manage sequential data such as signal, text and time series data.

Sequential Model

Why sequential?

If we consider sequential, the position of data can be meaningful.

Sequential Model: The model for dealing with sequential data.

• Input: Sequence

• Output: Sequence or Label

Example of sequential data

• Speech recognition
• Music generation
• Named entity recognition
• Machine translation

The difference between NN vs RNN

There are two main differences between Neural network and Recurrent neural network.

1. Inputs, outputs can be different lengths in Neural Network.
2. Doesn’t share feataures learned across different position of features.

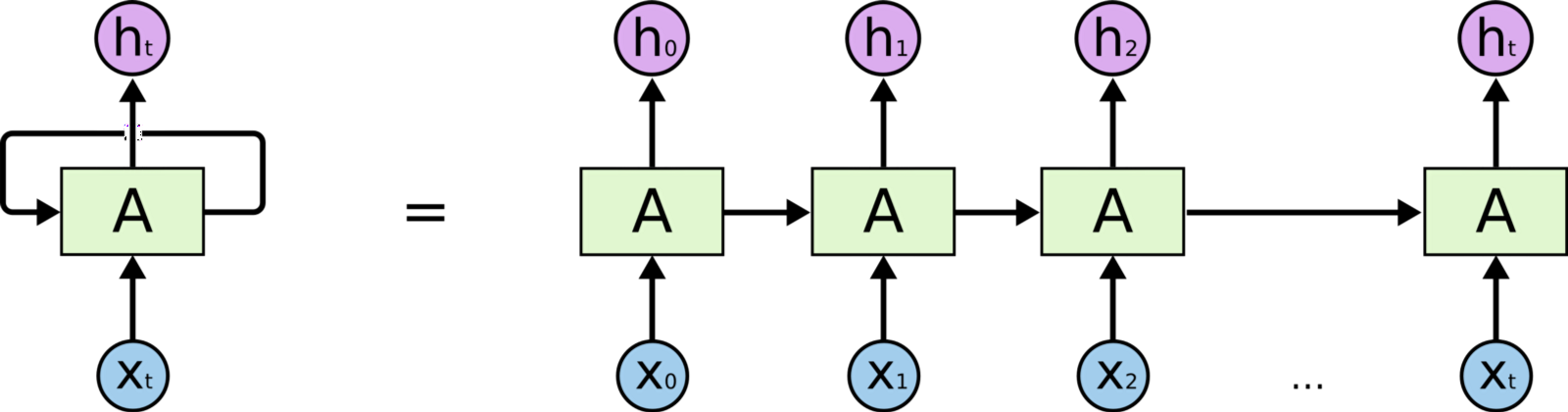
Concept of RNN

The idea of Recurrent Neural Network is the sequence of output can be defined by previous output and sequence input.

Like the image below, a folded node will work recurrently by delivering its output to itself.

And In the unfolded version, the inputs of current node are the output of previous node and the sequence input, $x_t$.

Let’s see the equation of RNN to see the detail.

\[\begin{align} & a^{<0>} = \vec{0} \\ & a^{<1>} = g(W_{aa}a^{<0>} + W_{ax}x^{<1>} + b_a) \\ & \hat y^{<1>} = g(W_{ya}a^{<1>} + b_y) \\ & \vdots \\ & a^{<t>} = g(W_{aa}a^{<t-1>} + W_{ax}x^{<t>} + b_a) \\ & \hat y^{<t>} = g(W_{ya}a^{<t>} + b_y) \end{align}\]

Above equation can be simplified like the below.

\[\begin{align} & a^{<t>} = g( \begin{bmatrix} W_{aa} & W_{ax} \end{bmatrix} \cdot \begin{bmatrix} a^{<t-1>} \\ x^{<t>} \end{bmatrix} + b_a ) \\ & \hat y^{<t>} = g(W_{ya} \cdot a^{<t>} + b_y) \end{align}\]

Weights

• $W_{aa}$ is the shared weights for next node.
• $W_{ya}$ is the shared weights for output.

Output

• In $a$, $g()$ is tanh or ReLU commonly.
• In $\hat y$, $g()$ is sigmoid or softmax (depending on the label)

Memory Cells

the output of a recurrent neuron at time step $t​$ is a function of all the inputs from previous time steps, so it has a form of memory.

Input and Output Sequences

RNN can simultaneously take a sequence of inputs and produce a sequence of outputs.

Limitation of RNN

Vanishing/exploding gradient problem

When you try to train RNN on long sequences, you suffer vanishing or exploding gradient.

Solution

1. good parameter initialization
2. nonsaturating activation functions(e.g. ReLU)
3. Batch Normalization
4. Gradient Clipping
5. Faster optimizer

LSTM(Long Short-Term Memory)

Even if the sequence is enough long without vaninshing/exploding gradient, The effect of first input will getting smaller to last input. It can cause the problem like missing context.

For example, When we want to train the text model, the RNN model can be trained well for grammar but not context. The sentence generated by our model is not good to remember contextual information.

To solve this proble, LSTM is designed to remeber the long and short term memory through the time series.

\[\begin{align} i_{(t)} &= \sigma(W_{xi}^T \cdot x_{(t)} + W_{hi}^T \cdot h_{(t-1)} + b_i) \\ f_{(t)} &= \sigma(W_{xf}^T \cdot x_{(t)} + W_{hf}^T \cdot h_{(t-1)} + b_f) \\ o_{(t)} &= \sigma(W_{xo}^T \cdot x_{(t)} + W_{ho}^T \cdot h_{(t-1)} + b_o) \\ g_{(t)}& = \tanh(W_{xg}^T \cdot x_{(t)} + W_{hg}^T \cdot h_{(t-1)} + b_g)\\ c_{(t)} &= f_{(t)} \otimes c_{(t-1)} + i_{(t)} \otimes g_{(t)}\\ y_{(t)} &= h_{(t)} = o_{(t)} \otimes \tanh(c_{(t)}) \end{align}\]

• $c_{(t)}$ is for long-term memory status.

  $c_{(t)}$ will drop some memories through the forget gate, and get some memories through the input gate.

• $h_{(t)}$ is for short-term memory status.

The output of $\tanh$ is between -1 and 1. So, the output value can be remebered for short-time.

The output of $\sigma$ is between 0 and 1. So, the output value can be decreased through the time step.

GRU(Gated Recurrent Unit)

The GRU cell is a simplified version of the LSTM cell, and it seems to perform just as well.

\[\begin{align} z_{(t)} &= \sigma(W_{xz}^T \cdot x_{(t)} + W_{hz}^T \cdot h_{(t-1)} + b_z) \\ r_{(t)} &= \sigma(W_{xr}^T \cdot x_{(t)} + W_{(hr)}^T \cdot h_{(t-1)} + b_r)\\ g_{(t)} &= \tanh(W_{xg}^T \cdot x_{(t)} + W_{hg}^T \cdot (r_{(t)} \otimes h_{(t-1)}) + b_g) \\ h_{(t)} &= (1-z_{(t)}) \otimes h_{(t-1)} + z_{(t)} \otimes g_{(t)} \end{align}\]

• Both state vectors are merged into a single vector $h_{(t)}$
• Both state vectors are merged into a single vector h_{(t)}.
• A single gate controller controls both the forget gate and the input gate. If the gate controller output is 1, the input gate is one and the forget gate is closed. If it output is 0.
• There is no output gate. the full state vector is output at every time step.