현대포트폴리오 이론 기반의 분산투자 with python

read

투자에서 유명한 격언 중 “계란을 한바구니에 담지말라.” 가 있다.

현대 포트폴리오 이론은 위의 격언처럼 투자에서 상관관계가 낮은 여러 종목으로 포트폴리오를 구성하면, 분산 투자 전보다 위험을 감소시킬 수 있다는 이론이다.

현대 포트폴리오 이론을 기반으로 투자 포트폴리오를 생성하고 평가하는 방법과 python 구현 코드에 대하여 소개하고자 한다.

해당 코드 및 정보는 위키피디아¹와 블로그 포스트²를 참조하여 작성하였습니다.

현대 포트폴리오 이론

시장에 참여하는 투자자들이 모두 합리적이고, 자산 간의 상관계수가 낮은 포트폴리오를 구성하면 분산이 감소함에 따라 이득을 얻을수 있다고 본다.

현대 포트폴리오 이론은 아래와 같은 가정을 가지고 있다.

투자자는 위험회피성향을 가지고, 기대효용 극대화를 목표
거래 비용과 세금은 고려 사항에서 제외
모든 투자자는 투자에 필요한 정보는 모두 동등하게 접근할 수 있음
평균 분산 기준: 기대 수익은 평균으로 측정하며, 위험은 분산으로 측정

많은 투자자들이 합리적인 투자가 아닌 투자를 하고 있고, 개인과 기업간의 정보의 비대칭성은 존재하기 때문에 주식시장은 위와 같은 과정과는 괴리가 있다.

현대 포트폴리오 이론의 목적은 위와 같은 가정아래 어떻게 투자자가 주어진 위험에 비해 자신의 기대 수익을 극대화할 수 있는지에 대한 이론이다.

투자자가 감수할수 있는 위험이 커질경우, 기대 수익률은 증가한다.

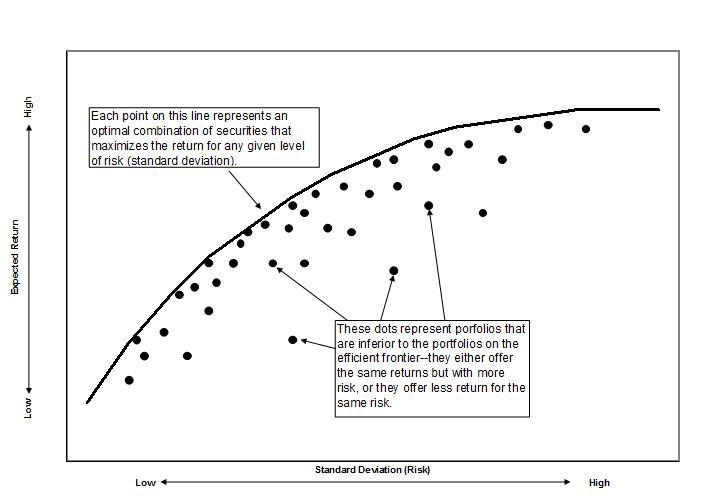
efficient_frontier

수익과 위험

N개의 주식으로 구성된 포트폴리오에서 기대수익률과 위험은 아래와 같은 수식으로 계산 가능하다.

포트폴리오의 기대 수익

기대 수익은 각각의 주식의 비중과 수익률을 곱한 것의 합과 같다.

\[E(R_p) = \sum_i w_i E(R_i)\]

포트폴리오의 위험(분산)

포트폴리오에서 위험(분산)은 포트폴리오의 변동성(표준편차)에 비례한다.

양으로 발산하는 분산은 초과수익률이지만, 음으로 발산하는 분산은 기대수익률에 대비한 위험으로 고려된다.

\[\sigma^2_p = \sum_i \sum_j w_iw_j \sigma_i \sigma_j p_{ij}\]

행렬로 표현하면 아래와 같다. $\sigma_p^2 = w^T \cdot \Sigma \cdot w \\ \Sigma= \text{covariance matrix of assets}$

포트폴리오 평가

샤프지수(Share ratio)

샤프지수(Share ratio)는 위험 대비 투자 수익률을 계산하는 지표로 사용된다.

\[\begin{align} \ & \text{Sharpe Ratio} = \frac{R_p R_{rf}}{\sigma_p} \\ \\ R_p =& \text{ Expected portfolio/asset return}\\ R_{rf} =& \text{ Risk-free rate of return}\\ \sigma =& \text{ Portfolio/asset standard deviation} \end{align}\]

변동성(Volatility)

변동성은 포트폴리오의 위험(분산, $\sigma^2$)에 대한 표준편차($\sigma$) 값이다.

python 구현

해당 코드의 기능은 아래와 같다.

동일 기간(M) 동안의 ETF 데이터 N개를 무작위 표본 추출
N개에 무작위 가중치 할당
해당 포트폴리오 평가
반복

데이터

데이터는 Naver 금융에서 수집한 한국 ETF 데이터의 종가(Closed price)를 사용하였다.

총 169개의 ETF 데이터에 대해서 거래 가능일 기준으로 정렬하여 Null 값이 없는 데이터만 추려서 사용하였다.

def get_etf_data(etf_name):
    etf_data = pd.read_csv('etf_data/' + etf_name, date_parser='TRD_DT')
    etf_data['date'] = etf_data['TRD_DT']
    return etf_data.set_index('date')

데이터 예시

ARIRANG 200선물레버리지	ARIRANG ESG우수기업	ARIRANG S&P;글로벌인프라	ARIRANG 고배당저변동	ARIRANG 고배당주채권혼합	ARIRANG 글로벌MSCI(합성 H)
2016-09-29	20110.0	NaN	NaN	10165.0	10130.0
		$\vdots$
2018-02-09	27820.0	9855.0	9720.0	11865.0	10695.0
2018-02-12	28400.0	9845.0	9675.0	11890.0	10725.0
2018-02-13	28875.0	9805.0	9810.0	11810.0	10700.0
		$\vdots$
2018-03-20	30805.0	9970.0	9650.0	11670.0	10625.0
2018-03-21	30855.0	9955.0	9630.0	11650.0	10630.0

포트폴리오의 유니버스(N)개에 대해서 일정 기간동안(M)의 행렬 형태의 데이터를 사용였다.

소스코드

class PortfolioManager:
    def __init__(self, data):
        self.data = data
        self.backtesting = dict()
        
    def get_randomized_weights(self, size):
        randomized_values = np.random.random([size])
        return randomized_values / sum(randomized_values)
    
    def get_sample_selected_ticker(self, num_of_tickers, min_exist):
        while True:
            selected_tickers = np.random.choice(data.columns, num_of_tickers)

            selected_data = self.data[selected_tickers]
            exist_range = selected_data.notnull().as_matrix().astype(int).mean(axis=1) == 1
            exist_percent = sum(exist_range)/len(exist_range)

            if sum(exist_range) > min_exist:
                return selected_data[exist_range][:min_exist]

    def get_variance(self, sample_data_returns, weights):
        cov_matrix_portfolio = sample_data_returns.cov() * 250
        variance = np.dot(weights.T, np.dot(cov_matrix_portfolio, weights))
        return variance
    
    def get_annual_returns(self, sample_data_returns, weights):
        annual_returns = sample_data_returns.mean() * 250
        expected_return = np.sum(annual_returns * weights)
        return expected_return
    
    def evaluate_porfolio(self, tickers, weights, num_of_tickers, display=False):
        sample_data_returns = selected_tickers.pct_change()
        
        #variance
        portfolio_variance = self.get_variance(sample_data_returns, weights)
        
        # standard deviation
        portfolio_volatility = np.sqrt(portfolio_variance)
        
        # Expected return
        expected_return = self.get_annual_returns(sample_data_returns, weights)
        sharp_ratio = expected_return / portfolio_volatility
        
        if display:
            print(sample_data.columns)
            print('Variance of Portfolio', str(round(portfolio_variance, 4) * 100) + '%')
            print('Variance of Risk', str(round(portfolio_volatility, 4) * 100) + '%')
        
            sample_data_returns.plot(figsize=(20,14))
        
        portfolio_dic = dict()
        selected_tickers_name = [ticker.split('.')[0] for ticker in selected_tickers.columns]

        portfolio_dic['tickers'] = selected_tickers_name
        portfolio_dic['weights'] = weights
        portfolio_dic['volatility'] = portfolio_volatility
        portfolio_dic['return'] = expected_return
        portfolio_dic['sharpe'] = sharp_ratio
        
        return portfolio_dic
    
    def simulation_portfolio(self, selected_tickers, num_try, display=True):
        port_returns = []
        port_volatility = []
        sharpe_ratio = []
        stock_weights = []

        portfolio = {'returns': port_returns,
                     'volatility': port_volatility,
                     'sharpe_ratio': sharpe_ratio}
        selected_tickers_name = [ticker.split('.')[0] for ticker in selected_tickers.columns]
        
        for i in range(num_try):
            weights = pb.get_randomized_weights(num_of_tickers)
            portfolio_summary = pb.evaluate_porfolio(selected_tickers, weights, num_of_tickers)

            port_returns.append(portfolio_summary['return'])
            port_volatility.append(portfolio_summary['volatility'])
            sharpe_ratio.append(portfolio_summary['sharpe'])
            stock_weights.append(weights)

        for idx, symbol in enumerate(selected_tickers_name):
            portfolio[symbol + ' weight'] = [weights[idx] for weights in stock_weights]
            
        column_order = ['returns', 'volatility', 'sharpe_ratio'] + [stock+' weight' for stock in selected_tickers_name]
        df = pd.DataFrame(portfolio)
        df = df[column_order]
        
        min_volatility = df['volatility'].min()
        max_sharpe = df['sharpe_ratio'].max()
        
        sharpe_portfolio = df.loc[df['sharpe_ratio'] == max_sharpe]
        min_variance_port = df.loc[df['volatility'] == min_volatility]
        
        if display:
            # use the min, max values to locate and create the two special portfolios

            plt.style.use('seaborn-dark')
            df.plot.scatter(x='volatility', y='returns', c='sharpe_ratio',
                           cmap='RdYlGn', edgecolors='black', figsize = (10, 8), grid=True)
            plt.scatter(x=sharpe_portfolio['volatility'], 
                        y=sharpe_portfolio['returns'], 
                        c='red', marker='D', s=200)
            plt.scatter(x=min_variance_port['volatility'], 
                        y=min_variance_port['returns'], 
                        c='blue', marker='D', s=200)

            plt.xlabel('Volatility (Std. Deviation)')
            plt.ylabel('Expected Returns')
            plt.title('Efficient Frontier')
            plt.show()
        
        simulation_result = {
            'min_volatility_portfolio': min_variance_port.T,
            'sharpe_portfolio': sharpe_portfolio.T,
            'min_volatility': min_volatility,
            'max_sharpe': max_sharpe,
            'tickers': selected_tickers_name
        }
        
        return simulation_result

포트폴리오 시뮬레이션 예시

n번의 포트폴리오 조합을 시뮬레이션 한 후, 가장 위험대비 수익률이 좋았던 포트폴리오를 선별하는 코드이다.

pb = PortfolioManager(data)
simulation_results = list()
max_return1 = -100
max_return2 = -100
num_of_tickers = 20
min_data_size = 300
fitted_portfolio = [None, None]

for i in range(10):
    selected_tickers = pb.get_sample_selected_ticker(num_of_tickers, min_data_size)
    simulation_result = pb.simulation_portfolio(selected_tickers, 50000, display=True)
    
    candi_return1 = simulation_result['sharpe_portfolio'].T['returns'].get_values()[0]
    candi_return2 = simulation_result['min_volatility_portfolio'].T['returns'].get_values()[0]
    simulation_results.append(simulation_result)

    if candi_return1 > max_return1:
        max_return1 = candi_return1
        fitted_portfolio[0] = simulation_result

    if candi_return1 > max_return2:
        max_return2 = candi_return2
        fitted_portfolio[1] = simulation_result

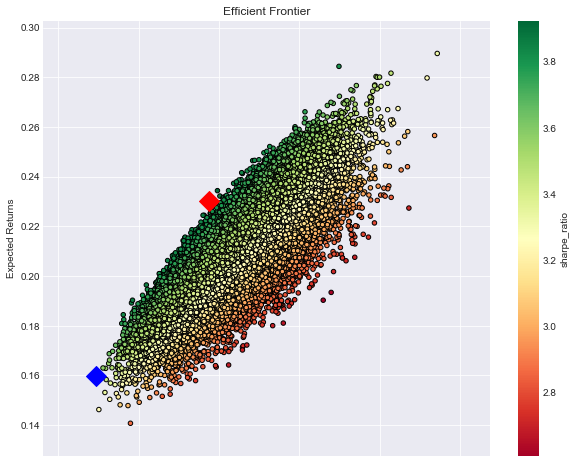
efficient_frontier_1

파란색 마커: 최소 변동성 포트폴리오 (안정적인 포트폴리오)
빨간색 마커: 최대 샤프지수 포트폴리오 (위험대비 수익률이 높은 포트폴리오)

Portfolio 결과 예시

Profolio number	6349
returns	0.106142
volatility	0.075177
sharpe_ratio	1.411897
TIGER 200 IT weight	0.012159
ARIRANG 스마트베타 Momentum weight	0.068125
$\vdots$
TIGER 200에너지화학레버리지 weight	0.014770
SMART 중국본토 중소형 CSI500(합성 H) weight	0.078324
KBSTAR 우량업종 weight	0.081562

결론

현대 포트폴리오 이론과 몬테카를로 시뮬레이션 기법을 이용하여 국내 ETF에 대한 분산투자 포트폴리오를 구성하는 방법을 소개해보았다.

위에서는 단순화를 위해서 가중치를 랜덤으로 하였고, 최소 가중치나 최대 가중치는 고려하지 않았다.

섹터별로 유니버스를 구분
단순한 종가가 아닌 feature 값 사용
머신러닝 기반의 모델 포트폴리오 생성

추후 좀 더 발전된 모델에서는 위와 같은 사항을 고려한 포트폴리오를 구성할 수 있을 것이다.

https://ko.wikipedia.org/wiki/포트폴리오_이론 ↩
https://medium.com/python-data/effient-frontier-in-python-34b0c3043314 ↩