read

머신러닝을 이용한 자산 배분 알고리즘의 하나로 계층형 리스크 패리티에 대해서 소개하고자 합니다. 해당 내용은 Advances in Financial Machine Learning¹ 내용을 참고하였습니다.

Introduction

포트폴리오를 구성하는 목적은 각기 상관관계가 낮은 자산들을 구성하여 전체 포트폴리오의 위험을 낮추기 위함입니다. Hierarchical Risk Parity 모델을 소개하기 전에 기존 자산 배분 모델 두 가지를 간단하게 설명하려고 합니다.

Risk Parity

리스크 패리티(Risk Parity)는 모든 자산이 동일한 변동성(Risk)을 가지도록 자산 배분을 하는 전략입니다.

Mean Variance Optimization

마코위츠에 의해 체계화된 현대 포트폴리오 이론의 기반이 되는 전략입니다. 목표는 기대수익률 대비해서 분산을 최소화하도록 비중을 할당 합니다.

투자하는 자산들이 각각 독립적이라고 한다면 위의 두 전략이 유효할 수 있습니다. 하지만, 우리가 다양한 종목을 투자할 때 종목 간에 움직임이 비슷한 경우에는 위의 두 방식이 정상적으로 동작하지 않을 수 있습니다.

A, B, C, D라는 자산이 있다고 하면, A, B, C, D 각각 자산의 변동성이 다르기 때문에 동일한 비중으로 설정한다고 하더라도 포트폴리오의 리스크를 낮추지 못하는 경우도 있습니다. 리스크 패리티 전략에서는 각 자산의 변동성의 역수만큼을 비중으로 하여, 각 자산이 포트폴리오에 미치는 영향도를 동일하도록 설정합니다.

자산이 포트폴리오에 미치는 영향도 = 자산의 변동성 $\times$ 자산의 비중

자산 Asset $i$가 포트폴리오 내의 비중을 $w_i$ 미치는 영향도를 $\sigma(w_i)$ 이라고 하면, 리스크 패리티 모델에서는 N 개의 자산으로 구성된 포트폴리오 전체 위험도 $\sigma$는 $\sigma(w_k) \times N$ 과 동일합니다.

\[\sigma = \sum_i^N \sigma(w_i) \\ \sum_i^N w_i =1, w_i \gt 0 \\\]

hierarchical Risk Parity

HRP의 동작은 3가지로 절차로 진행됩니다.

1. 각 자산간의 거리 계산 (Distance metric)
2. 거리 유사도에 따른 대각화 (Diagonalization)
3. 비중할당 (Weighting)

포트폴리오 내의 자산들을 계층화하고 계층화된 그룹이 포트폴리오에 미치는 영향도의 역수만큼을 weight로 설정합니다. 포트폴리오 내에 자산을 계층화 하기 위해서는 임의의 두 자산에 대한 거리를 계산해야 합니다. x, y의 상관 계수가 음의 상관 관계나 양의 상관 관계를 가진다고 하면 두 자산의 거리는 가깝다고 할 수 있습니다. 두 자산의 상관계수가 0에 가까울수록 두 자산의 거리가 멀어집니다.

포트폴리오 내에 N개의 자산에 대해서 각 두개의 조합에 대한 거리 행렬을 계산하고, 이를 기반으로 계층을 설정할 수 있습니다.

1. Distance Metric

각 자산간의 거리는 각 자산의 상관계수 값을 거리 값으로 인코딩하여 계산합니다.

인코딩된 거리(d) $0 \le d \le 1$ 의 값을 갖습니다.

\[X = T \times N \\ \rho = Corr(X) \\ \text{distance} = \sqrt{\frac{(1-p)}{2}}\]

example

\[\left\{\rho_{i, j}\right\}=\left[\begin{array}{ccc} 1 & .7 & .2 \\ .7 & 1 & -.2 \\ .2 & -.2 & 1 \end{array}\right] \rightarrow\left\{d_{i, j}\right\}=\left[\begin{array}{ccc} 0 & .3873 & .6325 \\ .3873 & 0 & .7746 \\ .6325 & .7746 & 0 \end{array}\right]\]

2. Diagonalization

대각화는 각 자산들의 거리행렬의 거리값을 기준으로 거리가 가까운 자산과 먼 자산을 재귀적으로 교체하여 정렬합니다.

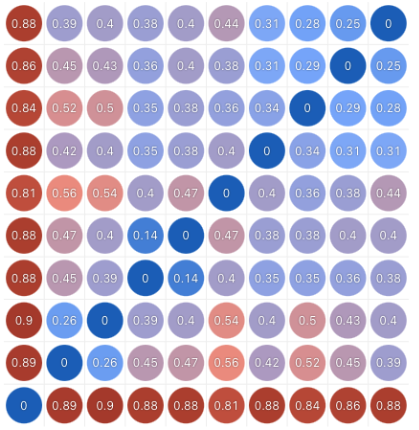
3. Weighting

비중은 각 클러스터의 리스크(분산)의 역수만큼을 해당 클러스터에 할당하고, 나머지 비중을 하위 클러스터에 재귀적으로 할당합니다.

Conclusion

기존의 포트폴리오 이론의 단점을 보완한 HRP (Hierarchical Risk Parity)에서 설명하였습니다.

HRP는 각 자산의 공분산을 거리로 수치화하여 위험을 최소화하는 포트폴리오를 구성하지만, 위험 대비 기대 수익률 값은 반영되지 않습니다. 각 자산 간의 거리 및 비중할당시에 기대수익률 값을 이용한 가중치를 활용한다면 좀 더 공격적인 포트폴리오를 구성할 수 있습니다.

Appendix

추가적인 수식 및 코드에 대한 설명을 추가하였습니다.

Appendix 1. Distance metric

\[\begin{align} d(x, y) &= \sqrt{\frac {1}{2}(1 - \rho(x, y))} \\ \hat{d}(x, y) &= \sqrt{\sum_{t=1}^T (X_t - Y_t)^2} \\ \text{where }&x=\frac{(X - \bar{X})}{\sigma(X)}, y=\frac{(Y - \bar{Y})}{\sigma(Y)} \\ \text{then, }& E(x)=0, \sigma(x) =1 \\ d(x, y) &= \sqrt{\sum_{t=1}^T(x_t - y_t)^2}\\ &= \sqrt{\sum_{t=1}^T x_t^2 + \sum_{t=1}^T y_t^2 - 2\sum_{t=1}^T x_ty_t} \\ &= \sqrt{T + T - 2T\rho(x, y)} \\ &= \sqrt{2T(1 - \rho(x, y))} \\ &= \sqrt{4T} \hat{d}(x,y) \end{align}\]

Appendix 2. Covariance

\[\begin{align} x &= \frac{X - \bar{X}}{\sigma(X)} \\ y &= \frac{Y - \bar{Y}}{\sigma(Y)} \\ E(x) &= \bar{x} = 0, \sigma(x) = 1 \\ \sigma(x, y) &= E(x - \bar{x})(y - \bar{y}) \\ \sigma(x, y) &= E(x^2) - E(x)^2 \\ \end{align}\]

1. Advances in Financial Machine Learning, Marcos Lopez de Prado (https://www.amazon.com/Advances-Financial-Machine-Learning-Marcos/dp/1119482089) ↩